MÉTALLOGRAPHIE - Essais physiques

MÉTALLOGRAPHIE - Essais physiques

Les principales caractéristiques physiques, en tout cas celles d’usage le plus courant, concernent respectivement la dilatation, la résistivité électrique, la capacité thermique massique, la conductivité thermique, les propriétés magnétiques, le pouvoir thermoélectrique. La mesure des variations de ces caractéristiques permet de déduire des informations concernant les évolutions structurales des métaux et alliages en fonction de la température et de la concentration. Les limites de stabilité des différentes phases des alliages en fonction de la composition et de la température, donc les diagrammes d’équilibre correspondant, peuvent être ainsi déterminés. Par ailleurs, elles permettent de caractériser les états structuraux métastables et d’analyser leur évolution en fonction de la température ou du temps; ainsi peuvent être étudiés: les états écrouis, les phénomènes de restauration et de recristallisation, l’influence de la trempe et du revenu, les processus de vieillissement et de précipitation, les transformations ordre-désordre, les mécanismes de frittage en système monophasé ou polyphasé.

1. Mesures de dilatation

Un solide métallique chauffé augmente de volume; la mesure linéaire d’une de ses dimensions traduit généralement aussi une expansion, sauf dans le cas de certaines directions cristallographiques, si le matériau considéré est anisotrope ou s’il se produit une transformation allotropique ou invariante. Comme il est plus commode de mesurer des variations de longueur que de volume, les paramètres habituellement employés caractérisent la dilatation linéaire.

La courbe de variation relative de longueur d’un échantillon en fonction de la température, soit = f (T) avec = (L 漣 L⁰)/L⁰, n’est pas linéaire. Par définition, le coefficient 見 de dilatation linéaire moyen est l’accroissement moyen de longueur par unité de longueur (prise à 0 ⁰C) et par degré, soit:

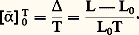De même, entre deux températures ¹ et ² on peut définir un coefficient moyen:

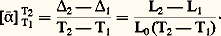Lorsque l’écart entre les températures ² et ¹ devient infinitésimal, il en est de même pour la variation de longueur concomitante. On définit alors un coefficient de dilatation linéaire vrai , soit:

Il existe une autre définition de ce coefficient de dilatation vrai lorsqu’on considère qu’il traduit le changement dimensionnel d’une longueur unitaire soumise à une modification de température égale à 1 ⁰C, soit:

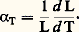Dans les cas où l’on est contraint de caractériser des variations de volume, on pourra utiliser des expressions similaires

correspondant aux coefficients de dilatation cubique moyen et vrai, soit:

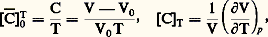avec: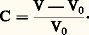

On peut donc écrire:

d’où: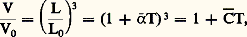

et finalement C 漣 力 3 見 漣. Les relations précédentes ne préjugent pas de la variation éventuelle de 見 ou de C en fonction de la température; or le fait même que les courbes = f (T) ne soient pas linéaires prouve que ces coefficients varient en fonction de T. On est donc conduit empiriquement à exprimer cette variation par une loi quadratique (des expressions encore plus complexes étant en fait plus rigoureuses):

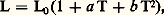donc, par exemple:

Les deux principales méthodes utilisées pour la détermination précise des variations dimensionnelles et des coefficients de dilatation sont la radiocristallographie et la dilatométrie.

Méthodes fondées sur la diffraction des rayons X

Les méthodes radiocristallographiques ont pour objet de déterminer les paramètres de la maille élémentaire du solide cristallin considéré, et l’évolution de ces paramètres en fonction de la température. À cette fin, des chambres « à chaud » ont été conçues; elles sont principalement de deux types: chambres photographiques et diffractomètres à compteur, comportant dans les deux cas une source de chauffage de l’échantillon. Ces deux types d’appareillage mettent en œuvre la méthode classique de Debye et Scherrer (cf. OPTIQUE CRISTALLINE - Diffraction par les cristaux). Toutes les méthodes fondées sur la diffraction des rayons X ont deux caractéristiques essentielles:

– elles sont en général très précises, sauf, peut-être, à température élevée, où l’élargissement des pics de diffraction entraîne une incertitude sur les mesures angulaires;

– elles permettent, dans le cas de matériaux de symétrie autre que cubique, de trouver les valeurs des paramètres suivant les axes principaux. On peut ainsi caractériser, quand elle existe, l’anisotropie de dilatation, tâche impossible aux autres méthodes, sauf dans le cas des monocristaux orientés.

Méthodes dilatométriques

On peut diviser les méthodes dilatométriques en deux groupes, selon que les variations dimensionnelles de l’échantillon sont ou non transmises par un poussoir.

Cas d’un échantillon isolé

Dans le cas d’un échantillon isolé, les mesures de longueur sont effectuées par voie optique; à l’aide de cathétomètres de précision on vise deux repères de l’éprouvette, elle-même placée dans un four. Quand l’échantillon, généralement de grande longueur, se dilate, on note l’écartement des repères et on trace ensuite la courbe = f (T). Cette méthode est une des plus anciennes, mais elle est d’un emploi peu commode, du fait que l’enregistrement ne peut être automatisé. Elle conserve néanmoins un certain intérêt dans deux cas: les mesures de dilatation à des températures très élevées (supérieures à 1 500 ⁰C) et les mesures extrêmement précices de dilatation au voisinage du point de fusion, permettant de caractériser l’influence des défauts ponctuels (lacunes) qui se traduit par un accroissement anormal de l’expansion thermique.

Cas d’un échantillon inséré dans un système de palpage

Un tel système de palpage comprend un support, fixé au bâti de l’appareil, dont une partie constitue une butée contre laquelle prend appui l’échantillon; l’autre extrémité de l’éprouvette est en contact avec un poussoir qui transmet les variations dimensionnelles à un dispositif de mesure (fig. 1). Le poussoir et le support sont constitués du même matériau (généralement de la silice jusqu’à 1 000 ⁰C, de l’alumine entre 1 000 et 1 500 ⁰C, et du tungstène au-delà de cette dernière température). Il y a donc compensation des variations dimensionnelles du poussoir et du support sauf sur une longueur égale à celle de l’échantillon, de sorte que le paramètre mesuré expérimentalement est égal à:

K( échantillon 漣 matériau support-poussoir), K désignant le coefficient d’amplification du dispositif de mesure.

Ces dispositifs de mesure amplificateurs sont principalement de deux types: des trépieds ou des comparateurs.

Deux dispositions de trépied sont possibles selon que celui-ci pivote autour d’un axe fixe défini par deux pointes – la troisième pointe étant sollicitée par le déplacement du poussoir appuyé contre l’échantillon (fig. 1 a) – ou que seule une des pointes du trépied repose sur une butée fixe appelée grain (fig. 1 b). Dans ce dernier cas, la méthode met en œuvre l’échantillon à étudier et un étalon de référence dont la dilatation est connue et réversible. Sur ce principe sont fondés les différents dilatomètres proposés par Chevenard et Bollenrath. Ils présentent l’avantage de pouvoir tracer des courbes directes ou différentielles (différence instantanée des dilatations respectives de l’échantillon et de l’étalon).

À ces trépieds sont associés soit des styles (enregistrement graphique), soit des miroirs (enregistrement photographique ou par suiveur de spot). Les coefficients d’amplification sont généralement limités à une valeur de l’ordre de 1 500.

On distingue trois groupes de comparateurs ayant chacun une spécificité propre: les comparateurs mécaniques, électroniques et optiques. Les comparateurs mécaniques sont des comparateurs classiques au centième ou au millième de millimètre, couramment utilisés pour les contrôles dimensionnels (cf. MESURE – Mesures mécaniques). Relativement peu coûteux, ils présentent par contre l’inconvénient de se prêter difficilement à un enregistrement automatique des variations.

Les comparateurs électroniques, généralement désignés par le terme de capteurs, sont soit de type inductif (transformateurs linéaires différentiels; cf. fig. 2), soit de type capacitif. Ils délivrent un signal électrique qu’il est facile d’amplifier, de sorte qu’il est théoriquement possible d’accéder à des amplifications très grandes. En pratique, il est toutefois difficile d’enregistrer des courbes dépouillables avec des amplifications supérieures à 10 000.

Les comparateurs optiques sont fondés sur deux méthodes: l’autocollimation et l’interférométrie. La première méthode a été en particulier mise en œuvre par Nickols: elle est fondée sur la séparation, par des miroirs, de deux faisceaux lumineux dont l’inclinaison est fonction des dilatations respectives de l’échantillon étudié et de cales étalons en silice. La seconde méthode est fondée sur la formation d’anneaux de Newton à partir d’une face plane de l’échantillon et d’une lentille auxiliaire: toute dilatation de l’échantillon se traduit par une modification du système d’anneaux (dilatomètre de Terpstra).

Ces méthodes s’appliquent essentiellement à des échantillons de faible dimension (de l’ordre de quelques millimètres au plus), souvent monocristallins. Elles permettent d’effectuer des mesures très précises (coefficients de dilatation à 10^-7 près), mais elles s’appliquent surtout à des mesures effectuées à une température voisine de l’ambiante ou, au plus, voisine de 500 ⁰C.

Pour effectuer des mesures à basse température (jusqu’à la température de l’hélium liquide: 4 K), les dilatomètres mettent en jeu des cryostats parfaitement régulés et des systèmes amplificateurs assez puissants, du fait que l’intervalle des températures explorées est seulement de 300 degrés environ; pour des grandes vitesses d’échauffement et surtout de refroidissement, on utilise des dilatomètres de trempe, particulièrement pour déterminer les caractéristiques d’évolution structurale des alliages métalliques: courbes T.T.T. (transformation, temps, température), T.R.C. (trempe en refroidissement continu), R.I.T. (revenu isotherme après trempe). Il faut alors compléter les montages dilatométriques par des systèmes de transfert automatique des échantillons d’un four à un autre ou d’un four dans un bain de trempe ou dans un moufle muni de buses de soufflage d’air pulsé. Les changements rapides de longueur et de température imposent l’emploi de systèmes de mesure électroniques à faible inertie (dilatomètre D.I.T.I.R.C. proposé par Georges Cizeron).

2. Mesures de résistivité

La résistivité d’un métal est principalement affectée par deux facteurs: la température et les impuretés. Quand la température varie dans un large domaine, la variation de la résistivité est compliquée et ne peut être décrite par une expression mathématique générale; aux températures supérieures à l’ambiante et pas trop proches du point de fusion, on peut, en première approximation, retenir une loi de la forme: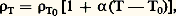

où ⁰ est une température de référence et 見 le coefficient de température que l’on peut définir à partir de la relation:

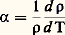( 見 est généralement de l’ordre de 4 . 10^-3 à 20 ⁰C).

D’autre part, aux très basses températures, la résistivité ne tend généralement pas vers zéro mais vers une limite finie qui est fonction des défauts présents dans le matériau (défauts d’ordre physique: lacunes, interstitiels ou dislocations ; ou d’ordre chimique: impuretés). Cela a conduit Augustus Matthiessen à exprimer la résistivité totale d’un matériau par la somme de deux termes, soit: 福 = 福^d + 福^T, 福^d étant un terme indépendant de la température et associé aux défauts, et 福^T le terme essentiellement fonction de la température. La résistivité peut également être affectée par l’application de contraintes: elle augmente généralement dans la direction de la contrainte appliquée 靖, mais le coefficient correspondant:

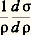reste le plus souvent faible, de l’ordre de 10^-6.

En général, il n’est pas nécessaire de mesurer les valeurs absolues de résistivité mais plutôt des variations de résistivité; d’autre part, on se contente le plus souvent de comparer entre elles des résistances, car le calcul exact de la résistivité implique la connaissance précise des dimensions de l’échantillon. Les mesures de résistances se font soit en courant continu, par mesures directes des tensions et des intensités (ponts de Wheatstone, de Thomson), soit en courant alternatif (pont de Wheatstone, mesure des inductances). Le principe de ces méthodes est exposé dans l’article MESURE – Mesures électriques et électroniques.

3. Mesures de la capacité thermique massique

Expérimentalement, on détermine généralement les paramètres C^p (capacité thermique molaire à pression constante) ou c ^p (capacité thermique massique à pression constante), et on en déduit C^v (capacité thermique molaire à volume constant) à partir de la relation:

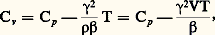où 塚 est le coefficient de dilatation cubique du matériau considéré (identique au paramètre C du paragraphe dilatations ); 廓 son coefficient de compressibilité, avec:

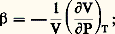V son volume et 福 sa masse volumique.

D’après les définitions précédentes on constate que la capacité thermique massique à pression constante peut être déduite, à température donnée, de la valeur de la pente au point correspondant de la courbe H = f (T). Parallèlement à cette première méthode d’évaluation, C^p peut aussi être directement mesuré.

Méthode des mélanges

La méthode des mélanges est fondée sur la détermination précise de l’élévation de température d’une enceinte (calorimètre) qui se produit lorsque l’on y introduit l’échantillon à étudier préchauffé à une température donnée.

Le calorimètre utilisé peut contenir de l’eau, de l’huile de paraffine... Ce mode opératoire ne convient que si la température de l’échantillon n’est pas trop élevée; en effet, dans le cas contraire, des pertes par évaporation ou éclaboussures sont à craindre. On a alors intérêt à faire tomber l’échantillon dans une cavité ménagée dans un bloc métallique, lui-même placé dans un vase Dewar logé dans un bain thermostaté. Toutefois, dans cette méthode, l’échange de chaleur par conduction est relativement lent et il est nécessaire d’utiliser des thermo-couples montés en série pour obtenir une mesure précise de l’évolution de la température.

La méthode des mélanges ne convient que si l’échantillon n’est pas le siège d’une transformation dans le domaine des températures étudiées ou du cours de la trempe (dans le cas contraire, seule la mesure directe de la capacité thermique massique est valable).

Les résultats obtenus conduisent le plus souvent à exprimer la variation d’enthalpie en fonction de la température par une équation de la forme:

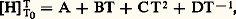d’où: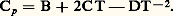

Mesure directe de la capacité thermique massique

Le principe de la mesure directe de la capacité thermique massique est de mesurer le changement de température subi par un échantillon en fonction d’une petite variation de son énergie thermique. On peut opérer de deux façons, selon que l’on fournit ou que l’on extrait de la chaleur de façon continue ou discontinue.

Méthodes continues

Si la chaleur est fournie (ou extraite) de façon continue, on peut écrire:

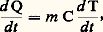soit: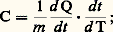

il suffit de mesurer simultanément des vitesses d’échange de chaleur et de variation de la température.

L’une des réalisations expérimentales a été proposée par C. Sykes; elle consiste à utiliser un échantillon cylindrique comportant un alésage borgne dans lequel est logé une résistance alimentée électriquement (fig. 3 a). Cet échantillon est placé dans un conteneur clos de sorte qu’il soit seulement guidé par des touches isolantes sans être en contact direct avec la paroi interne du conteneur. Ce dernier est à son tour placé dans un four. Soit T^c la température de la chambre du conteneur, chauffé progressivement à vitesse constante, et ^E la température de l’échantillon.

Si l’on n’alimente pas la résistance placée à l’intérieur de l’échantillon, ^E 麗 T^c ; par contre, grâce à un appoint d’énergie électrique, on peut annuler l’écart T^c 漣 ^E, auquel cas la vitesse d’échauffement de l’échantillon – soit d ^E/d t – est seulement fonction de l’énergie apportée par le circuit auxiliaire de chauffage. Comme on mesure en fait seulement T^c et (T^c 漣 ^E), on utilise la relation:

et on en déduit:

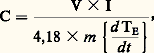V et I caractérisant la puissance délivrée à la résistance de chauffage.

Une autre méthode très classique est celle proposée par C. S. Smith. L’échantillon est logé dans un moufle réfractaire clos, lui-même placé dans un four (fig. 3 b); la puissance délivrée au four est telle que le flux de chaleur traversant la paroi du moufle soit constant quelle que soit la température, donc ⁰ est constant. On a alors, pendant l’intervalle de temps t ¹:

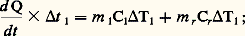m ¹ et m ^r étant les masses respectives de l’échantillon et du moufle, et ¹ l’élévation de température subie par l’échantillon. Si la même expérience est effectuée avec le moufle vide:

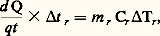d’où: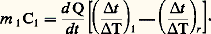

Pour éliminer le terme d Q/dt , il suffit de faire un essai avec un étalon de masse m ² et de capacité thermique massique c ²; on a alors:

En faisant le rapport de ces deux équations, on trouve: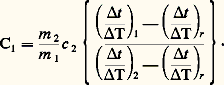

Il est naturellement nécessaire qu’au cours de ces différentes expériences l’écart ⁰ soit toujours le même.

Méthodes discontinues

La fourniture (ou l’extraction) d’une quantité discrète de chaleur entraîne une variation de la température de l’échantillon; le rapport de cette quantité de chaleur à l’écart de température fournit la capacité thermique massique. Pour minimiser les pertes, on opère généralement dans le vide et l’on s’arrange pour limiter à quelques degrés le changement de température de l’échantillon.

La méthode est surtout utilisable aux basses températures; elle a été préconisée en particulier par Hermann Walther Nernst et Arnold Thomas Eucken. L’échantillon est en deux parties: un premier cylindre, à la surface duquel est bobinée une résistance en platine, que l’on ajuste dans un second cylindre; l’ensemble est placé dans un conteneur, lui-même logé dans un four. Lorsque la température est stabilisée, on délivre une quantité connue d’énergie électrique au bobinage de platine, puis, dès la coupure du courant additionnel de chauffage, on mesure la variation de température en fonction du temps (à l’aide de ce même fil de platine faisant alors office de thermo-couple). La quantité de chaleur fournie Q est aisément calculée à partir du courant et de la tension utilisés. La variation de température est estimée par extrapolation graphique (fig. 4). Le courant ne passe que durant l’intervalle [t ¹, t ²]; la température n’étant supposée devenir uniforme qu’à partir du point R, on en déduit que le point P permet de connaître la température d’équilibre en fin de période de chauffe. On corrige enfin les pertes intervenant pendant le chauffage en ajoutant à la température définie par P¹ une quantité ¹ = P¹P²/2; d’où l’élévation de température corrigée T, et, finalement, C = Q/ T.

4. Mesures de la conductivité thermique

La distribution de la température dans les matériaux est conditionnée par l’écoulement de la chaleur en leur sein, c’est-à-dire par le transfert de l’énergie thermique d’atome à atome. On caractérise ce mode de transmission, appelé conduction, par un paramètre: la conductivité thermique. Soit un élément de volume de forme prismatique limité par deux sections parallèles de surface égale S, portées respectivement à deux températures différentes ¹et ²(T¹ 礪²) et distantes de x . La quantité de chaleur Q qui s’écoule d’une section vers l’autre (suivant la chute de température), pendant le temps t , est donnée par la formule:

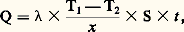( étant la conductivité thermique exprimée en W 練m^-1 練 ⁰C^-1). À la limite, si les sections sont très voisines, les quantités mises en jeu deviennent infinitésimales et on obtient:

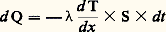(le signe moins est généralement introduit du fait que le gradient de température est négatif dans le sens de l’écoulement de chaleur).

Cette relation peut encore s’écrire, en posant:

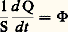(flux de chaleur par unité de surface):

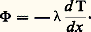On utilise parfois une notion similaire qui est la diffusivité thermique , définie par la relation:

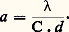a étant exprimé en m² 練 s^-1, C étant la chaleur spécifique du matériau et d sa masse volumique. Pour mesurer, il suffit donc de déteminer le flux de chaleur traversant une surface donnée, placée dans un gradient de température connu. À cet effet, on peut considérer principalement deux types d’écoulement de chaleur: unidirectionnel et radial; pour simplifier les mesures, il faut réaliser un état stationnaire et tenir compte des pertes thermiques éventuellement non compensées.

Écoulement unidirectionnel

Dans la méthode de Smith et Palmer, l’échantillon, sous forme de barreau, est entouré d’un tube métallique; l’ensemble est placé dans un four à gradient de température. Le rôle du tube périphérique est de minimiser les pertes radiales. Le flux de chaleur est mesuré à l’extrémité froide du barreau à l’aide d’un calorimètre à eau; le gradient de température est déterminé à l’aide de thermocouples. Un tel système implique d’employer un échantillon long et ne permet de mesurer que des valeurs moyennes de entre l’ambiante et une température plus ou moins élevée.

Dans la méthode de Schofield et Powell, pour s’affranchir de la sujétion consistant à maintenir l’une des extrémités de l’échantillon à faible température (calorimètre à eau), on place l’échantillon dans une enceinte isotherme et on lui fournit un excès connu d’énergie dans sa partie centrale. L’échantillon est alors constitué de deux parties, qui, une fois assemblées, ménagent entre elles une petite cavité dans laquelle est logée une résistance qui dissipe symétriquement de l’énergie électrique. Une variante de cette méthode consiste à intercaler un barreau étalon de conductivité connue entre deux barres du matériau étudié; le flux de chaleur est alors calculé à partir du gradient de température qui s’établit dans le barreau étalon.

Écoulement radial

L’échantillon, de forme cylindrique, comporte un alésage axial dans lequel est placé un élément chauffant. Des thermocouples, disposés dans la barre parallèlement à l’axe, mesurent le gradient radial de température. Les pertes longitudinales sont compensées par des enroulements chauffants placés aux extrémités de l’échantillon, ou en réalisant cet échantillon sous forme d’un assemblage de disques. Lorsque l’état stationnaire est atteint, on a:

(où q est la quantité de chaleur fournie sur la longueur l par unité de temps).

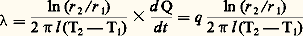L’avantage de cette méthode est qu’en entourant l’échantillon d’un tube chauffant on peut minimiser l’écart (T² 漣 ¹), et de ce fait effectuer des mesures dans d’étroits domaines de température (ceci le plus souvent au détriment de la précision de ces mesures).

Méthode de Kohlrausch

L’échantillon, sous forme de fil ou de barreau de faible section, est chauffé par effet Joule, ses extrémités ainsi que l’enceinte environnante étant maintenues à température constante ⁰. Il est préférable d’utiliser un courant alternatif pour éliminer un chauffage additionnel par effet Thomson. Dans ces conditions, le traitement mathématique du problème conduit à la relation:

où 靖 est la conductivité électrique du matériau, (V^m 漣 V⁰) la différence de potentiel mesurée entre le milieu et une des extrémités de l’échantillon, et (T^m 漣 ⁰) le gradient de température.

Lorsque les mesures sont effectuées à haute température, l’hypothèse selon laquelle les pertes sont proportionnelles à l’écart de température existant entre la surface et le milieu environnant doit être remplacée par celle d’un échange radiatif satisfaisant à la loi de Stefan-Boltzmann. La valeur de la conductivité thermique peut alors être déduite de la relation: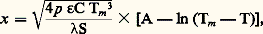

où p est le périmètre de l’échantillon, 﨎 le facteur d’émissivité, S la section droite, C la constante de Stefan-Boltzmann, A une constante d’intégration et x l’abscisse du point de l’échantillon où la température T est mesurée.

Il suffit pour cela de mesurer la pente de la droite:

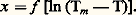Utilisation de la loi de Wiedemann-Franz-Lorenz

Bien qu’approximative dans le cas de certains métaux ou alliages – surtout à basse température –, la loi de Wiedemann-Franz-Lorenz peut être utilisée pour calculer la conductivité thermique, à des températures suffisamment élevées (T 礪 400 ⁰C), si l’on connaît par ailleurs la conductivité électrique du matériau. Cette loi s’exprime par la relation:

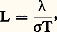L (égal à 2,45 練 10^-8 W 憐 行 練 K^-2) étant la constante de Lorenz, 靖 la conductivité électrique et T la température en K.

5. Mesures thermomagnétiques

Méthode de Gouý

La mesure de la susceptibilité magnétique par la méthode de Gouý nécessite l’utilisation d’échantillons ayant un volume de l’ordre de 10 cm³ ainsi que des valeurs élevées du champ (5 000 à 20 000 œrsteds), ce dernier devant être sensiblement constant dans un espace de dimensions raisonnables; cette méthode permet d’effectuer des mesures absolues de susceptibilité.

L’échantillon (de 100 à 150 mm de longueur) est un barreau de section uniforme S, une solution ou une poudre finement divisée (alors placées dans un tube de verre de section uniforme). Il est suspendu au fléau d’une balance sensible de sorte que son extrémité inférieure soit située au voisinage de l’axe d’un champ produit entre les pôles plats d’un électro-aimant, tandis que l’extrémité supérieure se trouve dans un champ H⁰. Soit k ² et k ¹ les susceptibilités magnétiques de l’échantillon et du milieu environnant. Compte tenu du fait que les composantes H^y et H^z du champ sont négligeables devant la composante H^x , la force agissant sur l’échantillon est égale à:

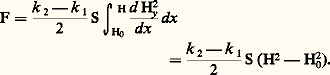Si H 力 10⁴ œrsteds et H⁰ 力 10² œrsteds, on pourra pratiquement négliger H²⁰ et on enregistrera, lorsque le champ est établi dans l’entrefer, une variation apparente de masse égale à:

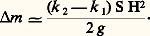D’où la valeur de k ² si tous les autres paramètres sont connus ou mesurés.

Méthode de Curie

La méthode de Curie ne met en œuvre que des quantités de substances faibles; elle permet d’effectuer des mesures en fonction de la température et nécessite des champs importants mais variant rapidement; les valeurs de susceptibilité obtenues ne sont généralement pas des valeurs absolues.

Les pôles de l’électro-aimant utilisé ne doivent pas être parallèles, de façon à ce que le champ ne soit pas constant; les pièces polaires peuvent être profilées de sorte que la courbe traduisant la variation de la quantité:

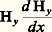présente une portion aplatieab (fig. 5 a). Dans de telles conditions, un échantillon de symétrie sphérique placé en E sera sollicité par une force égale à:

les deux composantes: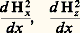

étant alors négligeables devant:

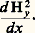Cette force pourra, comme dans la méthode précédente, être mesurée à l’aide d’une balance de torsion de sensibilité convenable et la susceptibilité magnétique k ² déterminée. Un des appareillages les plus classiques fondé sur un tel principe est la balance de Sucksmith représentée schématiquement dans la figure 5 a. L’échantillon est suspendu à un équipage comportant un anneau constitué d’un mince ruban métallique déformable; lorsque le champ est établi, l’anneau se déforme sous l’effet de la force F ^x et les deux miroirs m ¹ et m ² fixés sur cet anneau pivotent légèrement, ce qui provoque la déflexion d’un faisceau lumineux émis par une source S. La déviation angulaire du faisceau associée à F ^x peut être aisément calculée, et son expression est égale à:

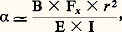où r est le rayon de l’anneau, E le module d’Young du matériau constituant l’anneau et I le moment d’inertie de la section du ruban.

À titre d’exemple, un second montage a également été employé: la balance à translation de Foëx et Forrer, décrite par le schéma de la figure 5 b. Lorsque l’électro-aimant crée le champ, l’équipage supportant l’échantillon a tendance à se déplacer; il revient à sa position initiale si on envoie un courant dans la bobine qui est susceptible de se mouvoir dans l’entrefer d’un aimant permanent A. De la valeur du courant traversant la bobine B on peut déduire la valeur de la force exercée, et par là celle de la susceptibilité cherchée.

6. Mesures du pouvoir thermoélectrique

Lorsque le pouvoir thermoélectrique P d’un matériau varie de façon régulière en fonction de la température, il suffit de l’associer à un matériau de référence pour réaliser un couple à partir duquel on mesurera les variations de force électromotrice en fonction de la température. Le platine est souvent employé comme étalon; dans le cas d’un alliage, on pourra aussi choisir un fil du métal de base comme étalon; de même, dans le cas d’un matériau écroui, on utilisera un fil du même matériau à l’état recuit. Pratiquement, il suffit de placer la soudure chaude du couple dans une enceinte chauffée et de maintenir les soudures à température constante (glace fondante, par exemple).

De cette façon, on pourra tracer la courbe E = f (T) et on en déduira facilement le pouvoir thermoélectrique:

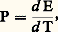puis la différence des coefficients 靖 de Thomson qui est proportionnelle à:

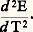Si par ailleurs les propriétés thermoélectriques varient rapidement avec la température ou sont sujettes à des discontinuités, il est préférable de mesurer directement le pouvoir thermoélectrique à l’aide d’une méthode différentielle (fig. 6). L’échantillon à étudier (sous forme de fil) est soudé à chacune de ses extrémités à deux fils B et C constitués de matériaux de référence. Dans une première expérience, les deux soudures chaudes sont portées à la même température (les soudures froides étant à la même température ⁰); les mesures de forces électromotrices entre B¹ et C¹ d’une part, B² et C² d’autre part, doivent donner exactement la même valeur. Dans une seconde expérience, l’une des soudures, S² par exemple, est portée à T + T; on mesure alors les forces électromotrices aux bornes B¹B² d’une part, C¹C² d’autre part. Soit E^AB et E^AC les valeurs trouvées, on a alors:

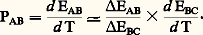E^AB est mesuré; E^BC peut être calculé en appliquant la règle additive:

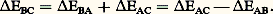D’où finalement:

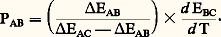Il faut donc connaître au préalable la valeur de P^BC, ce qui est facile si on a choisi pour thermocouple du type BC un système de référence classique.

7. Applications

Dilatométrie

Certains éléments métalliques – principalement des éléments de transition – présentent plusieurs variétés allotropiques qui ne sont stables que dans certains domaines de température; la transformation d’une variété en une autre s’accompagne d’une variation plus ou moins notable de volume spécifique, donc d’une anomalie dimensionnelle linéaire aisément observable par dilatométrie. Un exemple classique est celui du fer qui présente trois variétés allotropiques (fig. 7 a). Si l’on ajoute au fer des solutés de type alphagène, le diagramme d’équilibre correspondant présente une boucle caractéristique; le franchissement des limites du domaine 塚 peut également être observé par dilatométrie (fig. 7 b). Par contre, il est beaucoup plus difficile de mettre en évidence par cette méthode l’existence de la courbe limite de solubilité d’une solution solide primaire, si l’on coupe une telle courbe à basse température.

Par ailleurs, un des éléments caractéristiques des diagrammes d’équilibre est l’existence de paliers invariants (en particulier eutectoïdes): ces paliers sont très facilement mis en évidence, comme le montre la courbe de dilatation d’un acier à 0,88 p. 100 de carbone (fig. 7 c): anomalie de contraction à la chauffe pour une température de 735 ⁰C.

Lorsqu’on s’écarte des conditions d’équilibre, on peut observer avec un retard plus ou moins notable les évolutions structurales de phases instables; la dilatométrie de trempe permet de situer les différentes étapes de telles transformations: la figure 7 d en donne un exemple dans le cas d’un acier au chromemolybdène refroidi à une vitesse de 4 ⁰C 練 min^-1; la courbe 1 de la figure 7 d traduit l’évolution de l’austénite métastable, d’abord en perlite (ab ), puis en bainite (cd ).

Par ailleurs, un refroidissement plus énergique (trempe à l’eau glacée) transforme l’austénite des aciers suffisamment carbonés en martensite (courbe 2); la martensite est susceptible de se transformer par revenu. Cette évolution est complexe, et les divers stades qu’elle comporte se recouvrent le plus souvent; la figure 7 e représente schématiquement les trois stades principaux: stade I (relaxation des contraintes de trempe et formation du carbure 﨎), stade II (transformation de l’austénite résiduelle en ferrite plus carbures), stade III (formation de carbure 﨑, puis de cémentite Fe³C).

Ces exemples ne sont pas limitatifs, et l’on peut également tirer d’utiles renseignements de courbes dilatométriques anisothermes ou isothermes pour étudier le vieillissement d’alliages, le frittage d’agglomérés de poudres métalliques ou céramiques, etc.

Résistivité

Les mesures de résistivité peuvent aussi être utilisées avec fruit pour déterminer les limites des domaines d’existence des phases dans les diagrammes d’équilibre. En effet, la résistivité varie de façon non linéaire avec la concentration dans les domaines monophasés, et de façon linéaire dans des domaines biphasés: la figure 8 a illustre cette propriété et montre qu’en portant à une même température ⁰ divers alliages, élaborés à partir du même solvant A et de diverses concentrations en soluté B, puis en mesurant les variations de résistivité à cette température on déterminera successivement les points tels que a ,b ,c ...

D’autre part, les transformations structurales peuvent également être étudiées par mesures de résistivité. La figure 8 b, relative à un ferro-nickel à 30 p. 100 Ni illustre l’hystérèse importante qui accompagne la transformation austénite 燎 martensite.

De même, les phénomènes de vieillissement, au cours desquels se développe la précipitation de composés définis intermétalliques, donnent lieu à des variations aisément mesurables de la résistivité (en particulier, en condition isotherme, les cinétiques de précipitation peuvent être déterminées). La figure 8 c en donne un exemple dans le cas des alliages cuivre-béryllium à 2 p. 100 Be.

Enfin, une dernière illustration des possibilités offertes par les mesures de résistivité peut être évoquée dans le cas où l’on désire étudier la mobilité des défauts ponctuels. De tels défauts peuvent être créés entre autres par trempe brutale à partir de hautes températures ou par irradiation à basse température. Les lacunes ou les interstitiels en surnombre entraînent un accroissement de la résistivité (par rapport à la valeur mesurée dans les conditions d’équilibre). Par recuit progressif, on observe une restauration progressive de la résistivité qui met en fait en évidence plusieurs étapes au cours desquelles s’éliminent successivement les divers types de défauts engendrés. Une telle courbe est montrée en exemple dans la figure 8 d relative à un fil de tungstène irradié à 4 K.

Bien d’autres applications pourraient encore être mentionnées: par exemple l’étude des phénomènes de recristallisation des matériaux écrouis, les transformations ordre-désordre, etc.

Mesures thermomagnétiques

Les mesures thermomagnétiques sont essentiellement utilisées pour mettre en évidence les variations de l’intensité d’aimantation J ainsi que les points de Curie des phases ferromagnétiques. L’exemple du fer et de certains de ses alliages est très démonstratif. Si le matériau est très pur, la courbe thermomagnétique (courbe 1 de la fig. 9 a) ne révèle que la brusque variation de J au franchissement du point de Curie (770 ⁰C) – passage de l’état ferromagnétique à l’état paramagnétique variable. La transformation magnétique inverse s’effectue avec une très faible hystérésis. Si le métal est pollué par la présence d’une certaine quantité de carbone, on observe en outre à 210 ⁰C la transition magnétique de la cémentite Fe³C (courbe 2 de la fig. 9 a).

Si plusieurs phases magnétiques sont simultanément présentes, leurs différents points de Curie seront observés en même temps que les variations concomitantes de J: la figure 9 b, relative à l’évolution en chauffage d’un mélange de poudres de fer et de germanium (20 p. 100 atomique), révèle la formation de trois phases 見, 廓, 﨎. Il est d’autre part intéressant de souligner que les variations importantes de l’intensité d’aimantation ne sont pas obligatoirement associées à la transition magnétique d’une phase donnée; en effet, un changement de structure cristalline peut s’accompagner d’une modification importante de J: la transformation austénitemartensite des aciers maraging en est un exemple typique (fig. 9 c). Par contre, il est des cas où une transformation allotropique se produit sans anomalie, par exemple la transformation fer 見 paramagnétiquefer 塚 paramagnétique (fig. 9 a).

Parallèlement aux essais qui viennent d’être évoqués, il est également fréquent de tracer les courbes de variation de la susceptibilité magnétique en fonction de la température; on porte, en fait, généralement l’inverse de la susceptibilité, surtout si la phase étudiée est paramagnétique. La courbe 1 de la figure 9 d en donne un exemple dans le cas du fer: on voit ici tout l’intérêt de ce type de courbe qui montre la différence de comportement magnétique des phases paramagnétiques 見 et 塚, alors que les courbes J = f (T) (fig. 9 a) ne la révèlent pas. On remarquera d’ailleurs que le fait d’incorporer au fer une quantité suffisante (5 p. 100) d’un élément alphagène, comme le vanadium, supprime les transitions magnétiques (courbe 2, fig. 9 d).

Les changements d’état magnétique entraînent parfois des anomalies sur les courbes dilatométriques. Des exemples en sont donnés dans les figures 7 a, 7 c, 7 e: points T^c .

Pouvoir thermoélectrique

Dans les mesures classiques du pouvoir thermoélectrique, on réalise un couple en soudant un fil du métal à étudier à un fil de référence et on détermine la courbe E = f (T). Le tracé de la courbe dérivée fournit la variation du pouvoir thermoélectrique. Deux exemples en sont donnés dans le cas du nickel ou du fer associés au platine (fig. 10 a et b): on notera que les transitions magnétiques perturbent la variation du pouvoir thermoélectrique.

On peut également déterminer l’influence d’un élément d’addition sur le pouvoir thermoélectrique. La figure 10 c en donne trois exemples dans le cas des systèmes Zn-Cd, Cu-Ni ou Cu-Co: manifestement, la variation de P avec la concentration, dans le cas de solutions solides, n’est pas linéaire.

Le pouvoir thermoélectrique étant fortement affecté par la présence de soluté, même en faible quantité, dans un solvant, les mesures de P constituent un moyen très sensible d’étude de la précipitation. Enfin le pouvoir thermoélectrique est affecté par les contraintes internes (augmentation de P): sa mesure permet donc également de suivre les différentes étapes de la restauration et la recristallisation des matériaux écrouis.

Analyse thermique

Si on chauffe (ou si on refroidit) à vitesse constante un matériau métallique, la courbe température-temps présente des anomalies chaque fois qu’une évolution structurale se développe. Le tracé et l’interprétation de telles courbes constitue ce que l’on appelle l’analyse thermique, qui peut être simple ou différentielle.

Dans le cas de l’analyse thermique simple, on enregistre la variation de la température d’un échantillon soumis à des conditions régulières de chauffage ou de refroidissement. Cette méthode est surtout utilisée pour analyser la solidification des alliages métalliques portés initialement à l’état liquide. Dans la pratique, les phénomènes de surfusion peuvent fausser plus ou moins notablement les courbes T = f (t ); aussi est-il fréquent de tracer en fait des courbes:

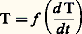ou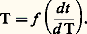

Dans ce dernier cas, on reporte les temps successifs nécessaires pour qu’une variation donnée de température se produise. L’allure des courbes théoriques et de celles expérimentalement obtenues sont indiquées sur la figure 11 a dans le cas d’une transformation ou d’un refroidissement.

Si l’évolution structurale a lieu en phase solide, l’énergie échangée est généralement trop faible pour que les mesures soient précises. Aussi est-il préférable d’utiliser un étalon de référence choisi dans un matériau restant inchangé dans l’intervalle de température où l’échantillon étudié se transforme. Cet étalon est disposé à proximité immédiate de l’échantillon – ou l’entoure –, et on mesure de façon continue la différence entre les températures des deux éprouvettes. Les courbes théoriques et celles effectivement obtenues sont schématisées sur la figure 11 b; on utilise également la courbe dérivée de la courbe T = f ( T) pour améliorer la précision sur la connaissance des températures de début et de sommet du pic.

Encyclopédie Universelle. 2012.